Is it enough to optimize CNN architectures on ImageNet? – Frontiers
1. Introduction
Deep convolutional neural networks (CNNs) are the core building block for most modern visual recognition systems and lead to major breakthroughs in many domains of computer perception in the past several years. Therefore, the community has been searching the high dimensional space of possible network architectures for models with desirable properties. Important milestones such as DanNet (Ciresan et al., 2012), AlexNet (Krizhevsky et al., 2012), VGG (Simonyan and Zisserman, 2015), HighwayNet (Srivastava et al., 2015), and ResNet (He et al., 2016) (a HighwayNet with open gates) can be seen as update steps in this stochastic optimization problem and stand testament that the manual architecture search works. It is of great importance that the right metrics are used during the search for new neural network architectures. Only when we measure performance with a truly meaningful metric is it certain that a new high-scoring architecture is also fundamentally better. So far, the metric of choice in the community has generally been the performance on the most well-known benchmarking dataset—ImageNet (Russakovsky et al., 2014).
More specifically, it would be desirable to construct such a metric from a solid theoretical understanding of deep CNNs. Due to the absence of a solid theoretical basis novel neural network designs are tested in an empirical fashion. Traditionally, model performance has been judged using accuracy point estimates (Krizhevsky et al., 2012; Zeiler and Fergus, 2014; Simonyan and Zisserman, 2015). This simple measure ignores important aspects such as model complexity and speed. Newer work addresses this issue by reporting a curve of the accuracy at different complexity settings of the model, highlighting how well a design deals with the accuracy vs. complexity tradeoff (Xie et al., 2017; Zoph et al., 2018).
Very recent work strives to improve the quality of the empiric evaluation even further. There have been attempts to use extensive empirical studies to discover general rules on neural network design (Hestness et al., 2017; Kaplan et al., 2020; Rosenfeld et al., 2020; Tuggener et al., 2020), instead of simply showing the merits of a single neural network architecture. Another line of research aims to improve empiricism by sampling whole populations of models and comparing error distributions instead of individual scalar errors (Radosavovic et al., 2019).
We acknowledge the importance of the above-mentioned improvements in the empirical methods used to test neural networks, but identify a weak spot that runs trough the above-mentioned work: the heavy reliance on ImageNet (Russakovsky et al., 2014) (and to some extent the very similar Cifar100 Krizhevsky and Hinton, 2009). In 2011, Torralba and Efros already pointed out that visual recognition datasets that were built to represent the visual world tend to become a small world in themselves (Torralba and Efros, 2011). Objects are no longer in the dataset because they are important, they are important because they are in the dataset. In this paper, we investigate how well ImageNet represents a diverse set of visual classification datasets—and present methods to improve said representation, such that CNN architectures optimized on ImageNet become more effective on visual classification beyond ImageNet. Specifically, our contributions are: (a) an extensive empirical study examining the fitness of ImageNet as a basis for deriving generally effective CNN architectures; (b) we show how class-wise subsampled versions of ImageNet in conjunction with the original datasets yield a 2.5-fold improvement in average error correlations with other datasets (c) we identify cumulative block depth and width as the architecture parameters most sensitive to changing datasets.
As a tool for this investigation we introduce the notion of architecture and performance relationship (APR). The performance of a CNN architecture does not exist in a vacuum, it is only defined in relation to the dataset on which it is used. This dependency is what we call APR induced by a dataset. We study the change in APRs between datasets by sampling 500 neural network architectures and training all of them on a set of datasets. We then compare errors of the same architectures across datasets, revealing the changes in APR (see Figure 1). This approach allows us to study the APRs induced by different datasets on a whole population of diverse network designs rather than just a family of similar architectures such as the ResNets (He et al., 2016) or MobileNets (Howard et al., 2017).
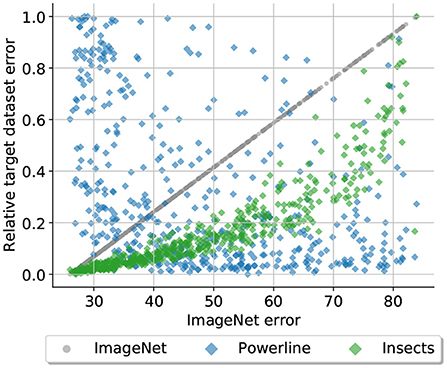
Figure 1. Is a CNN architecture that performs well on ImageNet automatically a good choice for a different vision dataset? This plot suggests otherwise: It displays the relative test errors of 500 randomly sampled CNN architectures on three datasets (ImageNet, Powerline, and Insects) plotted against the test error of the same architectures on ImageNet. The architectures have been trained from scratch on all three datasets. Architectures with low errors on ImageNet also perform well on Insects, on Powerline the opposite is the case.
All of our code, sampled architectures, complete training run data, and additional figures are available at https://github.com/tuggeluk/pycls/tree/ImageNet_as_basis.
2. Related work
2.1. Neural network design
With the introduction of the first deep CNNs (Ciresan et al., 2012; Krizhevsky et al., 2012) the design of neural networks immediately became an active research area. In the following years many improved architectures where introduced, such as VGG (Simonyan and Zisserman, 2015), Inception (Szegedy et al., 2015), HighwayNet (Srivastava et al., 2015), ResNet (He et al., 2016) (a HighwayNet with open gates), ResNeXt (Xie et al., 2017), or MobileNet (Howard et al., 2017). These architectures are the result of manual search aimed at finding new design principles that improve performance, for example increased network depth and skip connections. More recently, reinforcement learning (Zoph et al., 2018), evolutionary algorithms (Real et al., 2019) or gradient descent (Liu et al., 2019) have been successfully used to find suitable network architectures automatically. Our work relates to manual and automatic architecture design because it adds perspective on how stable results based on one or a few datasets are.
2.2. Empirical studies
In the absence of a solid theoretical understanding, large-scale empirical studies are the best tool at our disposal to gain insight into the nature of deep neural networks. These studies can aid network design (Collins et al., 2017; Greff et al., 2017; Novak et al., 2018) or be employed to show the merits of different approaches, for example that the classic LSTM (Hochreiter and Schmidhuber, 1997) architecture can outperform more modern models (Melis et al., 2018), when it is properly regularized. More recently, empirical studies have been used to infer more general rules on the behavior of neural networks such as a power-law describing the relationship between generalization error and dataset size (Hestness et al., 2017) or scaling laws for neural language models (Kaplan et al., 2020).
2.3. Generalization in neural networks
Despite their vast size have deep neural networks shown in practice that they can generalize extraordinarily well to unseen data stemming from the same distribution as the training data. Why neural networks generalize so well is still an open and very active research area (Dinh et al., 2017; Kawaguchi et al., 2017; Zhang et al., 2017). This work is not concerned with the generalization of a trained network to new data, but with the generalization of the architecture design progress itself. Does an architecture designed for a certain dataset, e.g. natural photo classification using ImageNet, work just as well for medical imaging? There has been work investigating the generalization to a newly collected test set, but in this case the test set was designed to be of the same distribution as the original training data (Recht et al., 2019).
2.4. Neural network transferability
It is known that the best architecture for ImageNet is not necessarily the best base architecture for other applications such as semantic segmentation (Long et al., 2015) or object detection (Chen et al., 2019). Researchers who computed a taxonomy of multiple visions tasks identified that the simmilarities between tasks did not depend on the used architecture (Zamir et al., 2019). Research that investigates the relation between model performance on ImageNet and new classification datasets in the context of transfer learning (Donahue et al., 2014; Razavian et al., 2014) suggests that there is a strong correlation which is also heavily dependent on the training regime used (Kornblith et al., 2019). Our work differs form the ones mentioned above in that we are not interested in the transfer of learned features but transfer of the architecture designs and therefore we train our networks from scratch on each dataset. Moreover do we not only test transferability on a few select architectures but on a whole network space.
2.5. Neural network design space analysis
Radosavovic et al. (2019) introduced network design spaces for visual recognition. They define a design space as a set of architectures defined in a parametric form with a fixed base structure and architectural hyperparameters that can be varied, similar to the search space definition in neural architecture search (Zoph et al., 2018; Liu et al., 2019; Real et al., 2019). The error distribution of a given design space can be computed by randomly sampling model instances from it and computing their training error. We use a similar methodology but instead of comparing different design spaces, we compare the results of the same design space on different datasets.
3. Datasets
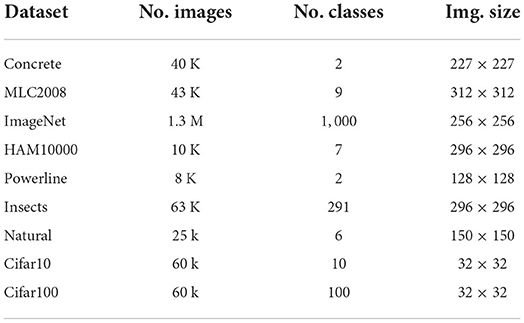
To enable cross dataset comparison of APRs we assembled a corpus of datasets. We chose datasets according to the following principles: (a) include datasets from a wide spectrum of application areas, such that generalization is tested on a diverse set of datasets; (b) only use datasets that are publicly available to anyone to ensure easy reproducibility of our work. Figure 2A shows examples and Table 1 lists meta-data of the chosen datasets. More detailed dataset specific information is given in the remainder of this chapter.

Figure 2. (A) Example images from each dataset. Images of Cifar10/100 are magnified fourfold, the rest are shown in their original resolution (best viewed by zooming into the digital document). (B) The structure of models in the AnyNetX design space, with a fixed stem and a head, consisting of one fully-connected layer of size c, (where c is the number of classes). Each stage i of the body is parametrised by di, wi, bi, gi, the strides of the stages are fixed with s1 = 1 and si = 2 for the remainder.
Concrete. Özgenel and Sorguç (2018) contains 40 thousand image snippets produced from 458 high-resolution images that have been captured from various concrete buildings on a single campus. It contains two classes, positive (which contains cracks in the concrete) and negative (with images that show intact concrete). With 20 thousand images in both classes the dataset is perfectly balanced.
MLC2008. Shihavuddin et al. (2013) contains 43 thousand image snippets taken form the MLC dataset (Beijbom et al., 2012), which is a subset of the images collected at the Moorea Coral Reef Long Term Ecological Research site. It contains images from three reef habitats and has nine classes. The class distribution is very skewed with crustose coralline algae (CCA) being the most common by far (see Figure A5A in Appendix 6.1).
ImageNet. Russakovsky et al. (2014) (The ILSVRC 2012 version) is a large scale dataset containing 1.3 million photographs sourced from flickr and other search engines. It contains 1, 000 classes and is well balanced with almost all classes having exactly 1, 300 training and 50 validation samples.
HAM10000. Tschandl et al. (2018) is comprised of 10 thousand dermatoscopic images, collected from different populations and by varied modalities. It is a representative collection of all important categories of pigmented lesions that are categorized into seven classes. It is imbalanced with an extreme dominance of the melanocytic nevi (nv) class (see Figure A5 in Appendix 6.1).
Powerline. Yetgin et al. (2017) contains images taken in different seasons as well as weather conditions from 21 different regions in Turkey. It has two classes, positive (that contain powerlines) and negative (which do not). The dataset contains 8, 000 images and is balanced with 4, 000 samples per classes.
Insects. Hansen et al. (2019) contains 63 thousand images of 291 insect species. The images have been taken of the collection of British carabids from the Natural History Museum London. The dataset is not completely balanced but the majority of classes have 100 to 400 examples.
Intel image classification. Bansal (2018) dataset (“natural”) is a natural scene classification dataset containing 25 thousand images and 6 classes. It is very well balanced with all classes having between 2.1 thousand and 2.5 thousand samples in the training set.
Cifar10 and Cifar100. Krizhevsky and Hinton (2009) both consist of 60 thousand images. The images are sourced form the 80 million tiny images dataset (Torralba et al., 2008) and are therefore of similar nature (photographs of common objects) as the images found in ImageNet, bar the much smaller resolution. Cifar10 has 10 classes with 6, 000 images per class, Cifar100 consists of 600 images in 100 classes, making both datasets perfectly balanced.
4. Experiments and results
4.1. Experimental setup
We sample our architectures form the very general AnyNetX (Radosavovic et al., 2020) parametric network space. The networks in AnyNetX consist of a stem, a body, and a head. The body performs the majority of the computation, stem and head are kept fixed across all sampled models. The body consists of four stages, each stage i starts with a 1 × 1 convolution with stride si, the remainder is a sequence of di identical blocks. The blocks are standard residual bottleneck blocks with group convolution (Xie et al., 2017), with a total block width wi, bottleneck ratio bi and a group width gi (into how many parallel convolutions the total width is grouped into). Within a stage, all the block parameters are shared. See Figure 2B for a comprehensive schematic. All models use batch normalization.
The AnyNetX design space has a total of 16 degrees of freedom, having 4 stages with 4 parameters each. We obtain our model instances by performing log-uniform sampling of di ≤ 16, wi ≤ 1, 024 and divisible by 8, bi ∈ 1, 2, 4, and gi ∈ 1, 2, …, 32. The stride si is fixed with a stride of 1 for the first stage and a stride of 2 for the rest. We repeatedly draw samples until we have obtained a total of 500 architectures in our target complexity regime of 360 mega flops (MF) to 400 MF. We chose a narrow band of complexities to allow for fair comparisons of architectures with minimal performance variation due to model size. We use a very basic training regime, input augmentation consists of only flipping, cropping and mean plus variance normalization, based on each datasets statistics. For training we use SGD with momentum and weight decay.
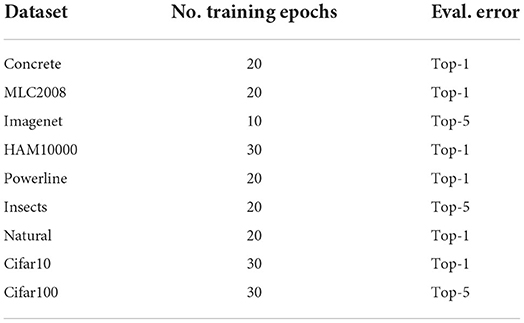
The same 500 models are trained on each dataset until the loss is reasonably saturated. The exact number of epochs has been determined in preliminary experiments and depends on the dataset (see Table 2). For extensive ablation studies ensuring the empirical stability of our experiments with respect to Cifar10 performance, training duration, training variability, top-1 to top-5 error comparisons, overfitting and class distribution see Sections 6.1.1–6.1.6 in Appendix 6.1. Supplementary material on the effect of pretraining and the structure of the best performing architectures can be found in Sections 6.2.1, 6.2.2 in Appendix 6.2.
4.2. Experimental results
We analyze the architecture-performance relationship (APRs) in two ways. For every target dataset (datsets which are not ImageNet) we plot the test error of every sampled architecture against the test error of the same architecture (trained and tested) on ImageNet, visualizing the relationship of the target dataset’s APR with the APR on ImageNet. Second, we compute Spearman’s ρ rank correlation coefficient (Freedman et al., 2007). It is a nonparametric measure for the strength of the relation between two variables (here the error on the target datasets with the error of the same architecture on ImageNet). Spearman’s ρ is defined on [−1, 1], where 0 indicates no relationship and −1 or 1 indicates that the relationship between the two variables can be fully described using only a monotonic function.
Figure 3 contains the described scatterplots with the corresponding correlation coefficients in the title. The datasets plotted in the top two rows show a strong (Insects) or medium (MLC2008, HAM10000, Cifar100) error correlation with ImageNet. This confirms that many classification tasks have an APR similar to the one induced by ImageNet, which makes ImageNet performance a decent architecture selection indicator for these datasets. The accuracies on Concrete are almost saturated with errors between 0 and 0.5, it is plausible that the variations in performance are due to random effects rather than any properties of the architectures or the dataset, especially so since the errors are independent of their corresponding ImageNet counterparts. Therefore, we refrain from drawing any further conclusions from the experiments on Concrete. This has implications for practical settings, where in such cases suitable architectures should be chosen according to computational and model complexity considerations rather than ImageNet performance, and reinforces the idea that practical problems may lie well outside of the ImageNet visual world (Stadelmann et al., 2018). The most important insight from Figure 3, however, is that some datasets have a slight (Cifar10) or even strong (Powerline, Natural) negative error correlation with ImageNet. Architectures which perform well on ImageNet tend perform sub-par on these datasets. A visual inspection shows that some of the very best architectures on ImageNet perform extraordinarily poor on these three datasets. We can conclude that the APRs can vary wildly between datasets and high performing architectures on ImageNet do not necessarily work well on other datasets.
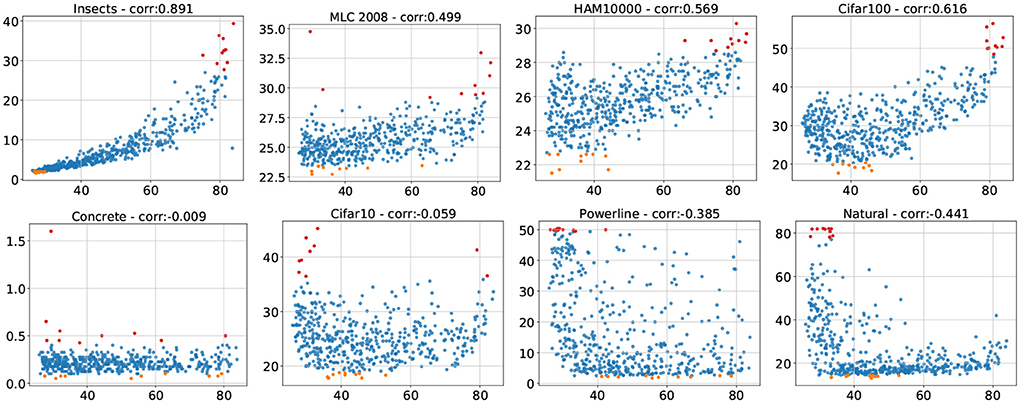
Figure 3. Test errors of all 500 sampled architectures on target datasets (y-axis) plotted against the test errors of the same architectures (trained and tested) on ImageNet (x-axis). The top 10 performances on the target datasets are plotted in orange and the worst 10 performances in red.
An analysis of the correlations between all datasets (see Figure A8 in Appendix 6.2) reveals that Powerline and Natural not only have low correlation with ImageNet but also with most of the other datasets making these two truly particular datasets. Interestingly is the correlation between Powerline and Naural relatively high, which suggests that there is a common trait that makes these two datasets behave differently. MLC 2008, HAM10000 and Cifar100 have a correlation of 0.69 with each other which indicates that they induce a very similar APR. This APR seems to be fairly universal since MLC 2008, HAM10000 and Cifar100 have a moderate to high correlation with all other datasets.
4.3. Impact of the number of classes
Having established that APR varies heavily between datasets, leaves us width the questions if it is possible to identify properties of the datasets themselves that influences its APR and if it is possible to control these factors to reduce the APR differences.
ImageNet has by far the largest number of classes among all the datasets. Insects, which is the dataset with the second highest class count, also shows the strongest similarity in APR to ImageNet. This suggests that the number of classes might be an important property of a dataset with respect to APR. We test this hypothesis by running an additional set of experiments on subsampled versions of ImageNet. We create new datasets by randomly choosing a varying number of classes from ImageNet and deleting the rest of the dataset (see Supplementary Section S3 for chosen classes). This allows us to isolate the impact of the number of classes while keeping all other aspects of the data itself identical. We create four subsampled ImageNet versions with 100, 10, 5, and 2 classes, which we call ImageNet-100, ImageNet-10, ImageNet-5, and ImageNet-2, respectively. We refer to the resulting group of datasets (including the original ImageNet) as the ImageNet-X family. The training regime for ImageNet-100 is kept identical to the one of ImageNet, for the other three datasets we switch to top-1 error and train for 40 epochs, to account for the smaller dataset size (see Section 4.3.1 in Appendix 6.1 for a control experiment that disentangles the effects of reduced dataset size and reduced number of classes).
Figure 4 shows the errors on the subsampled versions plotted against the errors on original ImageNet. APR on ImageNet-100 shows an extremely strong correlation with APR on ImageNet. This correlation significantly weakens as the class count gets smaller. ImageNet-2 is on the opposite end has errors which are practically independent from the ones on ImageNet. This confirms our hypothesis that the number of classes is a dataset property with significant effect on the architecture to performance relationship.

Figure 4. Error of all 500 sampled architectures on subsampled (by number of classes) versions of ImageNet (y-axis) plotted against the error of the same architectures on regular ImageNet (x-axis). The top 10 performances on the target dataset are plotted in orange and the worst 10 performances in red.
We have observed that the number of classes has a profound effect on the APR associated with ImageNet-X members. It is unlikely that simply varying the number of classes in this dataset is able to replicate the diversity of APRs present in an array of different datasets. However, it is reasonable to assume that a dataset’s APR is better represented by the ImageNet-X member closest in terms of class count, instead of ImageNet. We thus recreate Figure 3 with the twist of not plotting the target dataset errors against ImageNet, but against the ImageNet-X variant closest in class count (see Figure 5). We observe gain in correlation across all datasets, in the cases of MLC2008 or Cifar10 a quite extreme one. The datasets which have a strong negative correlation with ImageNet (Powerline, Natural) have slightly (Natural) or even moderately (Powerline) positive correlation to their ImageNet-X counterparts. A visual inspection shows that the best models on Imagenet-X also yield excellent results on Powerline and Natural, which was not the case for ImageNet. Table 3 shows the error correlations of all target datasets with ImageNet as well as with their ImageNet-X counterpart. The move from ImageNet to ImageNet-X more than doubles the average correlation (from 0.19 to 0.507), indicating that the ImageNet-X family of datasets is capable to represent a much wider variety of APRs than ImageNet alone.
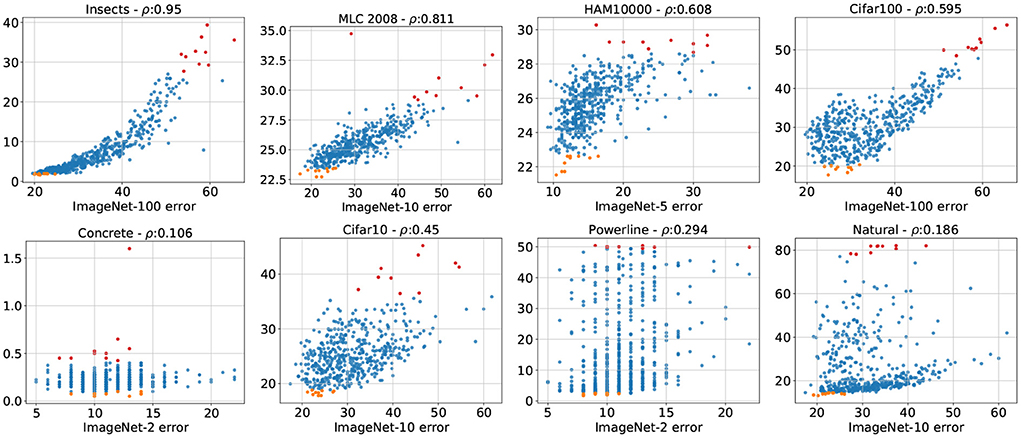
Figure 5. Test errors of all 500 sampled architectures on target datasets (y-axis) plotted against the test errors of the same architectures on the ImageNet-X (x-axis). The top 10 performances on the target dataset are orange, the worst 10 performances red.
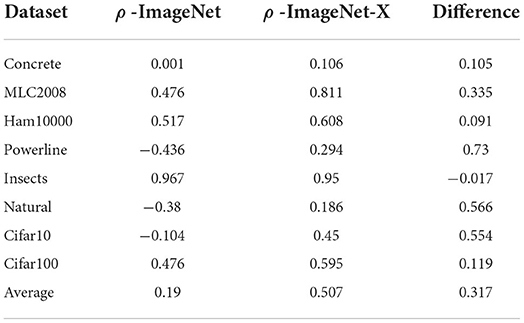
Table 3. Comparison of error correlations between target datasets and ImageNet as well as the closest ImageNet-X member.
4.3.1. Disentangling the effects of class count and dataset size
We showed how sub-sampled versions of ImageNet matching the number of classes of the target dataset tend to represent the APR of said target dataset far better. A side effect of downsampling ImageNet to a specific number of classes is that the total number of images present in the dataset also shrinks. This raises the question if the increase in error correlation is actually due to the reduced dataset size rather than to the matching class count. We disentangle these effects by introducing another downsampled version of ImageNet, Imagenet-1000-10. It retains all 1, 000 classes but only 10 examples per class resulting in a datastet with the same number of classes as ImageNet but with the total number of images of ImageNet-10. We train our population of architectures on ImageNet-1000-10 and show the error relationship of Cifar10, Natural, and Powerline with ImageNet-1000-10 (as well as with ImageNet and ImageNet-10 as a reminder) in Figure 6. The plots show that there are some correlation gains by using ImageNet-1000-10 over ImageNet, but the effect is far lower compared to ImageNet-10. This shows that downsampling size has a minor positive effect but the majority of the gain in APR similarity achieved trough class downsampling actually stems from the reduced the class number.
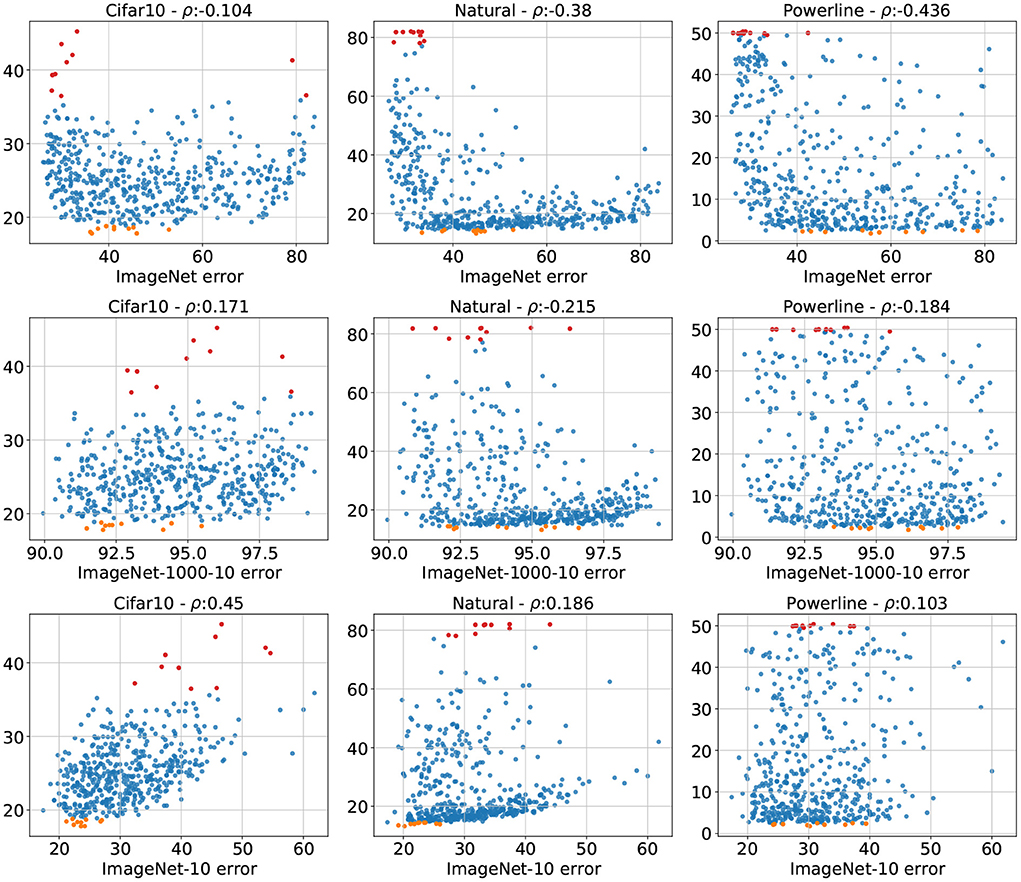
Figure 6. The errors of all 500 architectures on Cifar10, Natural, and Powerline plotted against the errors on ImageNet (top row), ImageNet-1000-10 (middle row) and ImageNet-10 (bottom row). We observe that class-wise downsampling has the largest positive effect on error correlation.
4.4. Identifying drivers of difference between datasets
The block width and depth parameters of the top 15 architectures for ImageNet (see Figure A7 in Appendix 6.2) follow a clear structure: they consistently start with low values for both block depth and width in the first stage, then the values steadily increase across the stages for both parameters. The error relationships observed in Figure 3 are consistent with how well these patterns are replicated by the other datasets. Insects shows a very similar pattern, MLC2008 and HAM10000 have the same trends but more noise. Powerline and Natural clearly break from this structure, having a flat or decreasing structure in the block width and showing a quite clear preference for a small block depth in the final stage. Cifar10 and Cifar100 are interesting cases, they have the same behavior as ImageNet with respect to block width but a very different one when it comes to block depth.
We thus investigate the effect of the cumulative block depth (summation of the depth parameter for all four stages, yielding the total depth of the architecture) across the whole population of architectures by plotting the cumulative block depth against the test error for the six above-mentioned datasets. Additionally, we compute the corresponding correlation coefficients. Figure 7A shows that the best models for ImageNet have a cumulative depth of at least 10. Otherwise there is no apparent dependency between the ImageNet errors and cumulative block depth. The errors of Insects do not seem to be related to the cumulative block depth at all. HAM10000 has a slight right-leaning spread leading to a moderate correlation, but the visual inspection shows no strong pattern. The errors on Powerline, Natural, and Cifar100 on the other hand have a strong dependency with the cumulative block depth. The error increases with network depth for all three datasets. with the best models all having a cumulative depth smaller than 10.
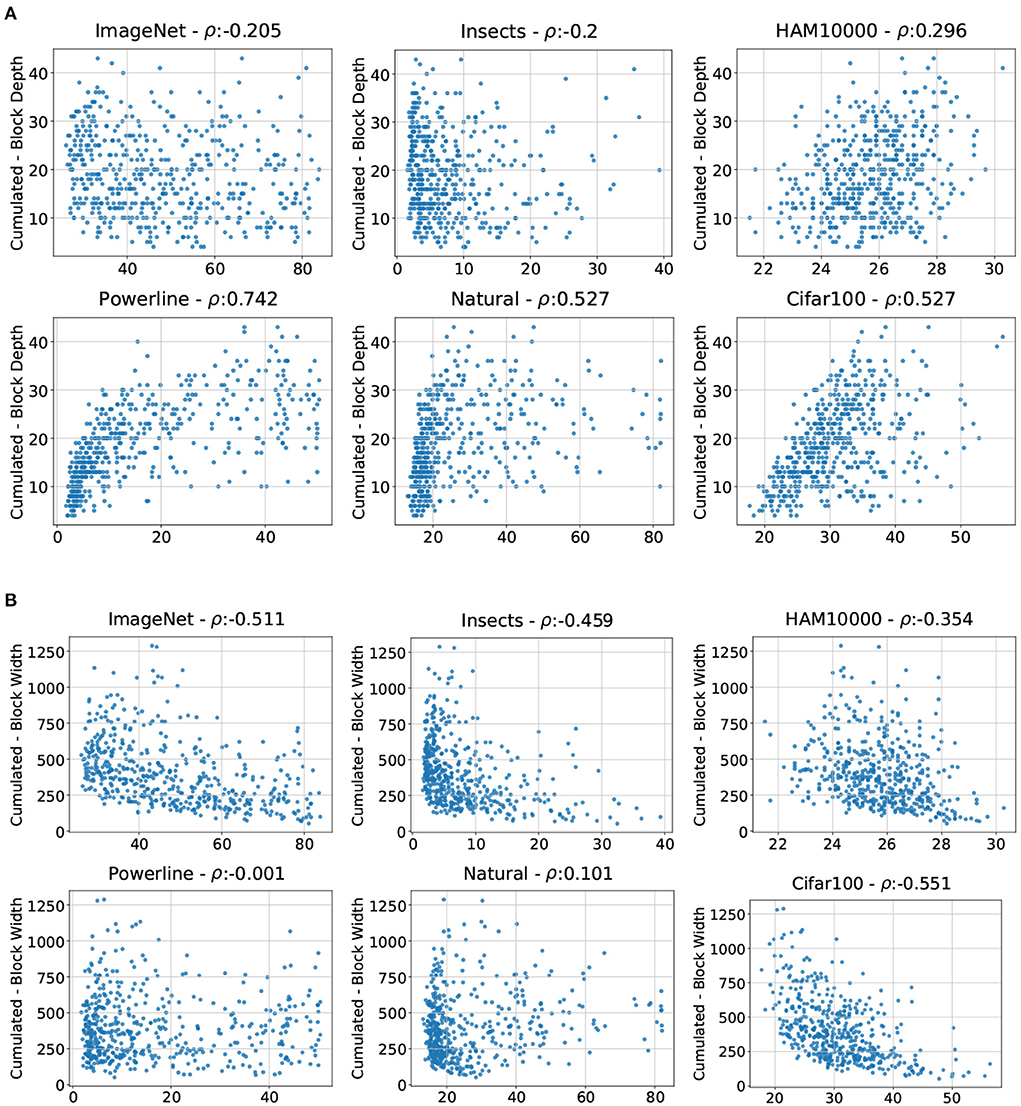
Figure 7. Errors of all 500 sampled architectures on ImageNet, Insects, HAM10000, Powerline, Natural, and Cifar100 (x-axis) plotted against the cumulative block (A) depths and (B) depths (y-axis).
We also plot the cumulative block widths against the errors and compute the corresponding correlation coefficients for the same six datasets (see Figure 7B). We observe that the ImageNet errors are negatively correlated with the cumulative block width, and visual inspection shows that a cumulative block width of at least 250 is required to achieve a decent performance. The errors on Insects and HAM10000 replicate this pattern to a lesser extent, analogous to the top 15 architectures. Powerline and Natural have no significant error dependency with the cumulative block width, but Cifar100 has an extremely strong negative error dependency with the cumulative block width, showing that it is possible for a dataset to replicate the behavior on ImageNet in one parameter but not the other. In the case of Cifar100 and ImageNet, low similarity in block depth and high similarity in block width yield a medium overall similarity of ARPs on Cifar100 and Imagenet. This is consistent with the overall relationship of the two datasets displayed in Figure 3.
Combining this result with the outcome of the last section, we study the interaction between the number of classes, the cumulated block depth and the cumulative block width. Table 4 contains the correlations between cumulative block depth/width and the errors on all members of ImageNet-X. With decreasing number of classes, the correlation coefficients increase for cumulative block depth and cumulative block width. Although the effect on cumulative block depth is stronger, there is a significant impact on both parameters. We therefore can conclude that both optimal cumulative block depth and cumulative block with can drastically change based on the dataset choice and that both are simultaneously influenced by the class count.
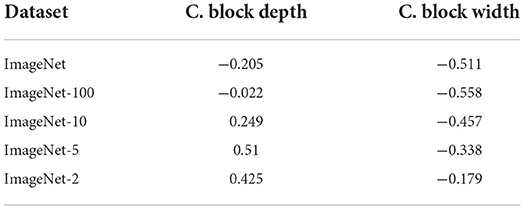
Table 4. Correlation of observed error rates with the cumulative block depth and width parameters for all ImageNet-X datasets.
5. Discussion and conclusions
5.1. ImageNet is not a perfect proxy
We have set out to explore how well other visual classification datasets are represented by ImageNet. Unsurprisingly there are differences between the APRs induced by the datasets. More surprising and worrying, however, is that for some datasets ImageNet not only is an imperfect proxy but a very bad one. The negative error correlations with Natural, Powerline and Cifar10 indicates that architecture search based on ImageNet performance is worse than random search for these datasets.
5.2. Varying the number of classes is a cheap and effective remedy
It is striking how much more accurately the ImageNet-X family is able to represent the diversity in APRs present in our dataset collection, compared to just ImageNet by itself. It has become commonplace to test new architectures in multiple complexity regimes (He et al., 2016; Howard et al., 2017), we argue for augmenting this testing regime with an additional dimension for class count. This simple and easy to implement extension would greatly extend the informative value of future studies on neural network architectures.
5.3. Visual variability is less important than anticipated
In the introduction we critiqued the over-reliance on ImageNet based on the limits of “visual world” it represents, since it only contains natural images and is mostly focused on animals and common objects. However, our results show that datasets with visually very different content such as Insects and HAM10000 have a high APR correlation with ImageNet. For Natural and Cifar10, which contain natural images, the opposite is the case. This shows that the visual domain of a dataset is not the central deciding factor for choosing the correct CNN architecture.
5.4. Future directions
A future similar study should shed light on how well the breadth of other domains such as object detection, segmentation or speech classification are represented by their essential datasets. If the representation is also insufficient it could be verified if the symptoms are similar and the varying the number of classes also helps covering more dataset variability in these domains.
A labeled dataset will always be a biased description of the visual world, due to having a fixed number of classes and being built with some systematic image collection process. Self-supervised learning of visual representations (Jing and Tian, 2019) could serve as remedy for this issue. Self-supervised architectures could be fed with a stream completely unrelated images, collected from an arbitrary number of sources in a randomized way. A comparison of visual features learned in this way could yield a more meaningful measure of the quality of CNN architectures.
5.5. Limitations
As with any experimental analysis of a highly complex process such as training a CNN it is virtually impossible to consider every scenario. We list below three dimensions along which our experiments are limited together with measures we took to minimize the impact of these limitations.
Data scope: We criticize ImageNet for only representing a fraction of the “visual world”. We are aware that our dataset collection does not span the entire “visual world” either but went to great lengths to maximize the scope of our dataset collection by purposefully choosing datasets from different domains, which are visually distinct.
Architecture scope: We sample our architectures from the large AnyNetX network space. It contains the CNN building blocks to span basic designs such as AlexNet or VGG as well as the whole ResNet, ResNeXt and RegNet families. We acknowledge that there are popular CNN components not covered, however, Radosavovic et al. (2020) present ablation studies showing that network designs sourced from high performing regions in the AnyNetX space also perform highly when swapping in different originally missing components such as depthwise convolutions (Chollet, 2017), swish activation functions (Ramachandran et al., 2018) or the squeeze-and-excitation (Hu et al., 2018) operations.
Training scope: When considering data augmentation and optimizer settings there are almost endless possibilities to tune the training process. We opted for a very basic setup with no bells an whistles in general. For certain such aspects of the training, which we assumed might skew the results of our study (such as training duration, dataset prepossessing etc.), we have conducted extensive ablation studies to ensure that this is not the case (see Sections 6.1.2 and 6.1.6 in Appendix 6.1).
Data availability statement
Publicly available datasets were analyzed in this study. This data can be found at: https://www.image-net.org/; https://www.kaggle.com/datasets/kmader/skin-cancer-mnist-ham10000; https://www.cs.toronto.edu/~kriz/cifar.html; https://www.kaggle.com/datasets/puneet6060/intel-image-classification; https://zenodo.org/record/3549369; https://data.mendeley.com/datasets/n6wrv4ry6v/8; https://data.mendeley.com/datasets/86y667257h/2.
Author contributions
LT was involved in every aspect of creating this work. TS and JS helped with the conception and shaping of the experimental design and acquired funds that contributed to this paper. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
This work has been financially supported by grants 25948.1 PFES-ES Ada (CTI), 34301.1 IP-ICT RealScore (Innosuisse) and ERC Advanced Grant AlgoRNN No. 742870. Open access funding provided by Zurich University of Applied Sciences (ZHAW).
Acknowledgments
We are grateful to Frank P. Schilling for his valuable inputs.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcomp.2022.1041703/full#supplementary-material
Footnotes
References
Bansal, P. (2018). Intel image classification.
Beijbom, O., Edmunds, P. J., Kline, D. I., Mitchell, B. G., and Kriegman, D. J. (2012). “Automated annotation of coral reef survey images,” in 2012 IEEE Conference on Computer Vision and Pattern Recognition (Providence, RI: IEEE Computer Society), 1170–1177.
Chen, Y., Yang, T., Zhang, X., Meng, G., Xiao, X., and Sun, J. (2019). “Detnas: backbone search for object detection,” in 32th Annual Conference on Neural Information Processing Systems, eds H. M. Wallach, H. Larochelle, A. Beygelzimer, F. d’Alché-Buc, E. B. Fox, and R. Garnett (Vancouver, BC), 6638–6648.
Chollet, F. (2017). “Xception: deep learning with depthwise separable convolutions,” in 2017 IEEE Conference on Computer Vision and Pattern Recognition (Honolulu, HI: IEEE Computer Society), 1800–1807.
Ciresan, D. C., Meier, U., and Schmidhuber, J. (2012). “Multi-column deep neural networks for image classification,” in 2012 IEEE Conference on Computer Vision and Pattern Recognition (Providence, RI: IEEE Computer Society), 3642–3649.
Collins, J., Sohl-Dickstein, J., and Sussillo, D. (2017). “Capacity and trainability in recurrent neural networks,” in 5th International Conference on Learning Representations (Toulon: OpenReview.net).
Dinh, L., Pascanu, R., Bengio, S., and Bengio, Y. (2017). “Sharp minima can generalize for deep nets,” in 34th International Conference on Machine Learning, eds D. Precup and Y. W. Teh (Sidney), 1019–1028.
Donahue, J., Jia, Y., Vinyals, O., Hoffman, J., Zhang, N., Tzeng, E., et al. (2014). “Decaf: a deep convolutional activation feature for generic visual recognition,” in 31th International Conference on Machine Learning (Beijing: JMLR.org), 647–655.
Freedman, D., Pisani, R., and Purves, R. (2007). Statistics (International Student Edition). Pisani, R. Purves, 4th Edn. New York, NY: WW Norton & Company.
Greff, K., Srivastava, R. K., Koutník, J., Steunebrink, B. R., and Schmidhuber, J. (2017). LSTM: a search space odyssey. IEEE Trans. Neural Netw. Learn. Syst. 28, 2222–2232. doi: 10.1109/TNNLS.2016.2582924
Hansen, O. L. P., Svenning, J.-C., Olsen, K., Dupont, S., Garner, B. H., Iosifidis, A., et al. (2019). Species-level image classification with convolutional neural network enable insect identification from habitus images. Ecol. Evol. 10, 737–747. doi: 10.1002/ece3.5921
He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Deep residual learning for image recognition,” in 2016 IEEE Conference on Computer Vision and Pattern Recognition (Las Vegas, NV: IEEE Computer Society), 770–778.
Hestness, J., Narang, S., Ardalani, N., Diamos, G. F., Jun, H., Kianinejad, H., et al. (2017). Deep learning scaling is predictable, empirically. CoRR, abs/1712.00409. doi: 10.48550/arXiv.1712.00409
Howard, A. G., Zhu, M., Chen, B., Kalenichenko, D., Wang, W., Weyand, T., et al. (2017). Mobilenets: efficient convolutional neural networks for mobile vision applications. CoRR, abs/1704.04861. doi: 10.48550/arXiv.1704.04861
Hu, J., Shen, L., and Sun, G. (2018). “Squeeze-and-excitation networks.” in 2018 IEEE Conference on Computer Vision and Pattern Recognition (Salt Lake City, UT: IEEE Computer Society), 7132–7141.
Kaplan, J., McCandlish, S., Henighan, T., Brown, T. B., Chess, B., Child, R., et al. (2020). Scaling laws for neural language models. CoRR, abs/2001.08361. doi: 10.48550/arXiv.2001.08361
Kawaguchi, K., Kaelbling, L. P., and Bengio, Y. (2017). Generalization in deep learning. CoRR, abs/1710.05468. doi: 10.48550/arXiv.1710.05468
Kornblith, S., Shlens, J., and Le, Q. V. (2019). “Do better imagenet models transfer better?” in 2019 IEEE Conference on Computer Vision and Pattern Recognition (Long Beach, CA: Computer Vision Foundation; IEEE), 2661–2671.
Krizhevsky, A., and Hinton, G. (2009). Learning Multiple Layers of Features From Tiny Images. Technical Report, University of Toronto.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). “Imagenet classification with deep convolutional neural networks,” in 26th Annual Conference on Neural Information Processing Systems, eds P. L. Bartlett, F. C. N. Pereira, C. J. C. Burges, L. Bottou, and K. Q. Weinberger (Lake Tahoe, CA), 1106–1114.
Liu, H., Simonyan, K., and Yang, Y. (2019). “DARTS: differentiable architecture search,” in 7th International Conference on Learning Representations (New Orleans, LA: OpenReview.net).
Long, J., Shelhamer, E., and Darrell, T. (2015). “Fully convolutional networks for semantic segmentation,” in 2015 IEEE Conference on Computer Vision and Pattern Recognition (Boston, MA: IEEE Computer Society), 3431–3440.
Melis, G., Dyer, C., and Blunsom, P. (2018). “On the state of the art of evaluation in neural language models,” in 6th International Conference on Learning Representations (Vancouver, BC: OpenReview.net).
Novak, R., Bahri, Y., Abolafia, D. A., Pennington, J., and Sohl-Dickstein, J. (2018). “Sensitivity and generalization in neural networks: an empirical study,” in 6th International Conference on Learning Representations (Vancouver, BC: OpenReview.net).
Özgenel, Ç, C. F., and Sorguç, A. G. (2018). “Performance comparison of pretrained convolutional neural networks on crack detection in buildings,” in ISARC. Proceedings of the International Symposium on Automation and Robotics in Construction (Berlin: IAARC Publications), 1–8.
Radosavovic, I., Johnson, J., Xie, S., Lo, W., and Dollár, P. (2019). “On network design spaces for visual recognition,” in International Conference on Computer Vision (Seoul: IEEE), 1882–1890.
Radosavovic, I., Kosaraju, R. P., Girshick, R. B., He, K., and Dollár, P. (2020). “Designing network design spaces,” in 2020 IEEE Conference on Computer Vision and Pattern Recognition (Venice: IEEE), 10425–10433.
Ramachandran, P., Zoph, B., and Le, Q. V. (2018). “Searching for activation functions,” in 6th International Conference on Learning Representations Workshop Track Proceedings (Vancouver, BC: OpenReview.net).
Razavian, A. S., Azizpour, H., Sullivan, J., and Carlsson, S. (2014). “CNN features off-the-shelf: an astounding baseline for recognition,” in 2014 IEEE Conference on Computer Vision and Pattern Recognition (Columbus, OH: IEEE Computer Society), 512–519.
Real, E., Aggarwal, A., Huang, Y., and Le, Q. V. (2019). “Regularized evolution for image classifier architecture search,” in The Thirty-Third AAAI Conference on Artificial Intelligence (Honolulu, HI: AAAI Press), 4780–4789.
Recht, B., Roelofs, R., Schmidt, L., and Shankar, V. (2019). “Do imagenet classifiers generalize to imagenet?” in 36th International Conference on Machine Learning, eds K. Chaudhuri and R. Salakhutdinov (Long Beach, CA), 5389–5400.
Rosenfeld, J. S., Rosenfeld, A., Belinkov, Y., and Shavit, N. (2020). “A constructive prediction of the generalization error across scales,” in 8th International Conference on Learning Representations (Addis Ababa: OpenReview.net).
Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S., Ma, S., et al. (2014). Imagenet large scale visual recognition challenge. CoRR, abs/1409.0575. doi: 10.48550/arXiv.1409.0575
Shihavuddin, A. S. M., Gracias, N., García, R., Gleason, A. C. R., and Gintert, B. (2013). Image-based coral reef classification and thematic mapping. Remote. Sens. 5, 1809–1841. doi: 10.3390/rs5041809
Simonyan, K., and Zisserman, A. (2015). “Very deep convolutional networks for large-scale image recognition,” in 3rd International Conference on Learning Representations, eds Y. Bengio and Y. LeCun (San Diego, CA).
Srivastava, R. K., Greff, K., and Schmidhuber, J. (2015). Highway networks. CoRR, abs/1505.00387. doi: 10.48550/arXiv.1505.00387
Stadelmann, T., Amirian, M., Arabaci, I., Arnold, M., Duivesteijn, G. F., Elezi, I., et al. (2018). “Deep learning in the wild,” in IAPR Workshop on Artificial Neural Networks in Pattern Recognition (Siena: Springer), 17–38.
Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S. E., Anguelov, D., et al. (2015). “Going deeper with convolutions,” in 2015 IEEE Conference on Computer Vision and Pattern Recognition (Boston, MA: IEEE Computer Society), 1–9.
Torralba, A., and Efros, A. A. (2011). “Unbiased look at dataset bias,” in 2011 IEEE Conference on Computer Vision and Pattern Recognition (Colorado Springs, CO: IEEE), 1521–1528.
Torralba, A., Fergus, R., and Freeman, W. T. (2008). 80 million tiny images: a large data set for nonparametric object and scene recognition. IEEE Trans. Pattern Anal. Mach. Intell. 30, 1958–1970. doi: 10.1109/TPAMI.2008.128
Tschandl, P., Rosendahl, C., and Kittler, H. (2018). The HAM10000 dataset: a large collection of multi-source dermatoscopic images of common pigmented skin lesions. CoRR, abs/1803.10417. doi: 10.1038/sdata.2018.161
Tuggener, L., Amirian, M., Benites, F., von Däniken, P., Gupta, P., Schilling, F.-P., et al. (2020). Design patterns for resource-constrained automated deep-learning methods. AI 1, 510–538. doi: 10.3390/ai1040031
Xie, S., Girshick, R. B., Dollár, P., Tu, Z., and He, K. (2017). “Aggregated residual transformations for deep neural networks,” in 2017 IEEE Conference on Computer Vision and Pattern Recognition (Honolulu, HI: IEEE Computer Society), 5987–5995.
Yetgin, Ö. E., Gerek, Ö. N., and Nezih, Ö. (2017). Ground truth of powerline dataset (infrared-ir and visible light-vl). Mendeley Data 8, 9. doi: 10.17632/twxp8xccsw.9
Zamir, A. R., Sax, A., Shen, W. B., Guibas, L. J., Malik, J., and Savarese, S. (2019). “Taskonomy: disentangling task transfer learning,” in International Joint Conference on Artificial Intelligence 2019, ed S. Kraus (Macao: ijcai.org), 6241–6245.
Zeiler, M. D., and Fergus, R. (2014). “Visualizing and understanding convolutional networks,” in 13th European Conference on Computer Vision, Proceedings, Part I, eds D. J. Fleet, T. Pajdla, B. Schiele, and T. Tuytelaars (Zurich: Springer), 818–833.
Zhang, C., Bengio, S., Hardt, M., Recht, B., and Vinyals, O. (2017). “Understanding deep learning requires rethinking generalization,” in 5th International Conference on Learning Representations (Toulon: OpenReview.net).
Zoph, B., Vasudevan, V., Shlens, J., and Le, Q. V. (2018). “Learning transferable architectures for scalable image recognition,” in 2018 IEEE Conference on Computer Vision and Pattern Recognition (Salt Lake City, UT: IEEE Computer Society), 8697–8710.
6. Appendix
6.1. Verifying the numerical robustness of our study
This Chapter we present additional studies designed to test for possible flaws or vulnerabilities in our experiments. We conduct these to further strengthen the empirical robustness of our results.
6.1.1. Stability of empirical results on Cifar10
The top-1 errors of our sampled architectures on Cifar10 lie roughly between 18 and 40, which is fairly poor, not only compared to the state of the art but also compared to performance that can be achieved with fairly simple models. This calls into question if our Cifar10 results are flawed in a way that might have lead us to wrong conclusions. We address this by running additional tests on Cifar10 and evaluate their impact on our main results. We get a goalpost for what performance would be considered good with our style of neural network and training setup by running the baseline code for Cifar10 published by Radosavovic et al. (2020). Table A1 shows that these baseline configurations achieve much lower error rates. We aim to improve the error results on Cifar10 in two ways: First we train our architecture population with standard settings for 200 epochs instead of 30 s, we replaced the standard network stem with one that is specifically built for Cifar10, featuring less stride and no pooling. Figure A1 shows scatterplots of the errors from all 500 architectures on Cifar10 against the errors on ImageNet and ImageNet-10. We can see that both new training methods manage to significantly improve the performance with a minimum top-1 error below 10 in both cases. More importantly can we observe that both new training methods have, despite lower overall error, a very similar error relationship to ImageNet. The error correlation is even slightly lower than with our original training (replicated in Figure A1, left row). We can also see that in all three cases the error relationship can be significantly strengthened by replacing ImageNet with ImageNet-10, this shows that tuning for individual performance on a dataset does not significantly impact the error relationships between datasets which further strengthens our core claim.

Figure A1. The Cifar10 test errors of all 500 architectures plotted against ImageNet (top row) and ImageNet-10 (bottom row), shown for our original Cifar10 training (left column), training with a Cifar10 specific stem in the architecture (middle column), and training for 200 epochs, which is roughly 6 times longer (right column). The plots show that the error correlation with ImageNet-10 is much larger in all three cases, confirming that optimizing for individual Cifar10 performance does not alter our core result.
6.1.2. Verifying training duration
Since we have a limited amount of computational resources and needed to train a vast number of networks we opted to train the networks up to the number of epochs where they started to saturate significantly in our pre-studies. As we have seen in Section 6.1.1 can the network performance still improve quite a bit if it is trained for much longer. Even though the improved performances on Cifar10 did not yield any results contradicting the findings of our study, we still deemed it necessary to closer inspect what happened in the later stages of training and thus performed a sanity check for Cifar10 as well as the other two datasets that show a negative error correlation with ImageNet—Powerline and Natural. Figure A2A shows the Cifar10 test error curves of 20 randomly selected architectures over 200 epochs. On the left side we see the same curves zoomed in to epochs 30 to 200. We see that the error decreases steadily for all architectures, the ranking among architectures barely changes past epoch 30. The relative performance between architectures and not absolute error rates are relevant for our evaluations, we can therefore conclude that the errors at epoch 30 are an accurate enough description of an architecture’s power.
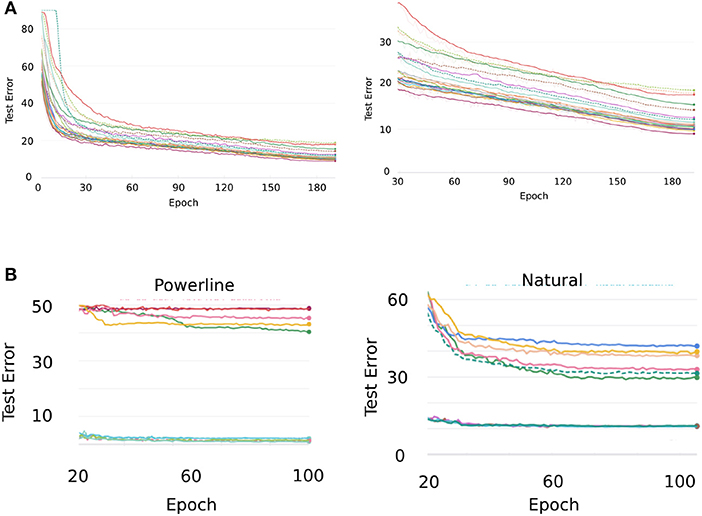
Figure A2. (A) Cifar10 test error curves of 20 randomly sampled architectures trained over 200 epochs (left). The same error curves but cut to epochs 30–200. (B) Test error curves of the five best and five worst models on Powerline and Natural, respectively, when training is continued to epoch 100.
For Powerline and Natural, we select the five best and five worst architectures, respectively and continue training them for a total of five times the regular duration. Figure A2B shows the resulting error curves. Both datasets exhibit minimal changes in the errors of the top models. On Natural we observe clear improvements on the bottom five models but similar to Cifar10 there are very little changes in terms of relative performance. Powerline exhibits one clear cross-over but for the remainder of the bottom five models the ranking also stays intact. Overall we can conclude that longer training does not have a significant effect on the APR of our datasets.
6.1.3. Impact of training variability
The random initialization of the model weights has an effect on the performance of a CNN. In an empirical study it would therefore be preferable to train each model multiple times to minimize this variability. We opted to increase the size of our population as high as our computational resources allow, this way we get a large number of measurements to control random effects as well as an error estimate of a large set of architectures. However, we still wanted to determine how much of the total variability is caused by training noise and how much is due to changing the architectures. We estimate this by selecting two of the sampled CNN designs, number 147 performing slightly above average with an error of e147 = 11.9 and number 122 performing slightly below average with e122 = 14.5. The quantiles of the error distribution from all 500 architectures are q0.25 = 11.53, q0.5 = 13.02 and q0.75 = 15.46 with an overall mean of μ = 13.9. We then train the architectures 147 and 122 each 250 times. Figure A3 shows the error distributions of both selected architectures as well as the overall distribution obtained from training each of the 500 architectures once. There is of course some variability within both architectures but both individual architectures produce very narrow densities and show essentially no overlap. We can therefore conclude that the effect of choosing an architecture is much greater than the variability caused by random training effects.
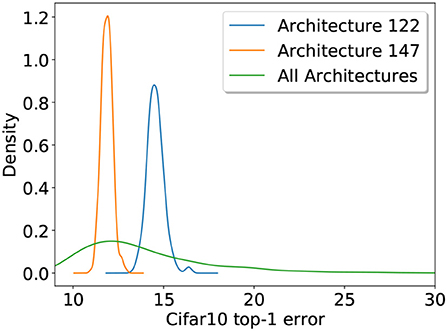
Figure A3. Error distributions on Cifar10 of two architectures (122, 147) both trained from scratch 250 times as well as the Cifar10 error distribution of all 500 architectures. The plot shows that the variability caused by changing architecture is much larger than the one caused by random training effects.
6.1.4. Relationship of top-1 with top-5 error on ImageNet, Insects and Cifar100
We opted to use top-5 error since it is the most widely reported metric for ImageNet and the top-5 numbers are therefore easy to interpret on that dataset. Many of our datasets have a significantly lower number of classes such that top-5 error makes little sense and we opted to use top-1 for those. This raises the question if comparing top-1 with top-5 errors introduces unwanted perturbations into our analysis. We therefore compare the top-1 and top-5 errors for the three datasets on which we use top-1 error (see Figure A4A). We see that the two metrics have an almost linear relationship for the ImageNet and Cifar100 datasets. More importantly are the top-1 to top-5 error graphs monotonically ascending for all three datasets, such that the ordering of architectures does not change when swapping between the two metrics. Since we are interested in the relative performances of our sampled architectures changing between top-1 and top-5 error does not impact our analysis.
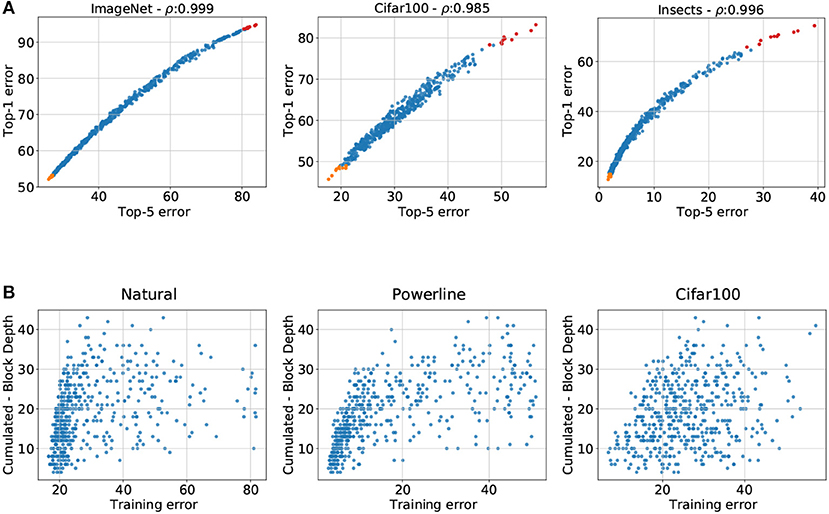
Figure A4. (A) Top-1 error plotted against top-5 error of all 500 architectures on ImageNet, Cifar100, and Insects. The plots reveal that on all three datasets the errors have a very close relationship: it is not perfectly linear but is monotonically ascending. (B) Training errors of the sampled architectures (x-axis) plotted against the cumulated block depth for the 3 datasets that have the lowest test errors on shallow architectures. We observe that for all three datasets shallow architectures also have the lowest training errors. Therefore overfitting is not the cause of this behaviour.
6.1.5. Overfitting of high-capacity architectures
The best architectures on Powerline, Natural and Cifar100 have a very small cumulated depth, so it is only natural to ask if the deeper architectures perform poorly due to overfitting. We address this concern by plotting the training errors of Powerline, Natural, and Cifar100 against the cumulative block depths (see Figure A4B). The training errors are strongly correlated with the cumulative block depth, just like the test errors. Plots of the cumulated block depth show almost the same structure for training and test errors. We can therefore exclude overfitting as a reason why the shallower networks perform better on Powerline, Natural, and Cifar100.
6.1.6. Impact of class distribution
MLC2008 and HAM1000 have a strong class imbalance. They both have one class which makes up a large amount of the dataset. In order to study the impact of an imbalanced class distribution, we created two new more balanced datasets out of the existing data the following way: we reduced the number of samples in the overrepresented class such that it has the same amount of samples as the second most common class. We call these datasets MLC2008-balanced and HAM10000-balanced. Their new class distributions can be seen in Figure A5A. We train our architecture population on MLC2008-balanced and HAM10000-balanced leaving the training configuration otherwise unaltered. Figure A5B shows the errors on the balanced datasets vs. the errors on the unbalanced counterparts.

Figure A5. (A) Class distributions of MLC2008, HAM10000, and their balanced versions. (B) Errors of all 500 sampled architectures on MLC2008-balanced and HAM1000-balanced (y-axis) plotted against the errors of their unbalanced counterparts (x-axis). The top 10 performances on the target dataset are plotted in orange, the worst 10 performances in red. We observe a clear positive correlation for both datasets, hence we conclude that the dataset imbalance has a limited impact on the APRs.
For both HAM10000 and and MLC2008, there is a strong correlation between the errors on the balanced and unbalanced datasets. We can therefore conclude that class imbalance is not a determining factor for the APRs of HAM10000 or MLC2008.
6.2. Additional ablation studies
6.2.1. Impact of Pretraining
The main objective of our study is to identify how well different CNN designs perform on varying datasets and if the best architectures are consistent across the datasets. For this reason we train all of our networks from scratch on each dataset. However, we cannot ignore that pretraining on ImageNet is a huge factor in practice and we therefore study its impact on our evaluations. To this end have we train all of our sampled architectures again on each dataset but this time we initialize their weights with ImageNet pretraining (we omit Concrete, which has very low errors even without pretraining). Figure A6 shows the errors of each dataset without (blue) and with (green) pretraining plotted against the ImageNet errors. The data shows a distinct trend: the overall performance improvement due to pretraining dictates how much stronger the ImageNet-correlation of the pretrained errors is compared to the errors without pretraining. For Cifar10 and Cifar100 where the performance gain with pretraining is low to moderate the error correlations do not drastically change. On the other end of the spectrum are Natural and Powerline, where pretraining leads to drasticall y lower errors. This in turn leads to much higher error correlation with ImageNet(the Powerline correlation can not grow significantly above 0 because the overall errors are so small across all architectures). We can conclude that our findings are still valid when pretraining is used, but their effects can be masked when pretraining is the most important factor contributing to the overall final performance.
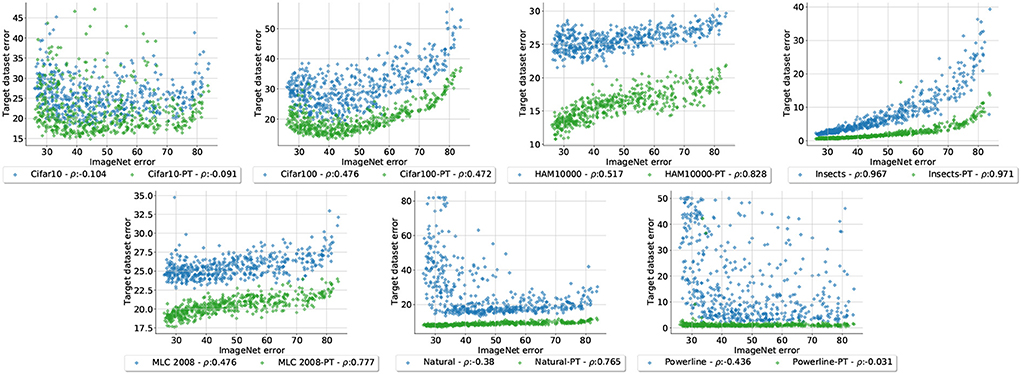
Figure A6. Errors form all 500 architectures trained from scratch (blue) as well as the same architectures pretrained on ImageNet (green), plotted against the respective ImageNet errors. We observe that the error correlation with ImageNet increases relative to the performance gain due to pretraining.
6.2.2. Structure of top performing architectures
Figure A7 shows the configuration of the top performing architecture in blue, as well as the mean and standard deviation of the top 15 configurations for every dataset. We observe that the top 15 architectures have very high variance in both bottleneck ratio and group width.
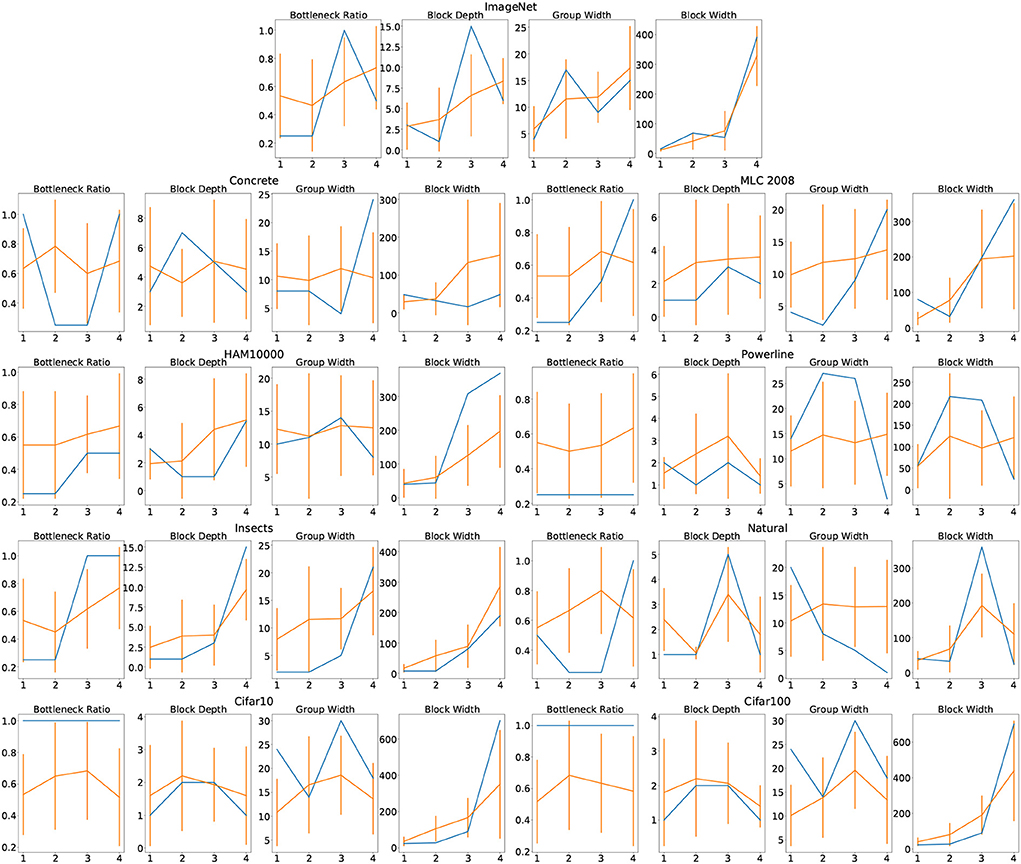
Figure A7. Configurations of the top-performing architectures, with the four stages depicted on the x-axis and the parameter values on the y-axis. The best architectures are shown in blue, the mean of the top 15 architectures is depicted in orange with with a vertical indication of one standard deviation.
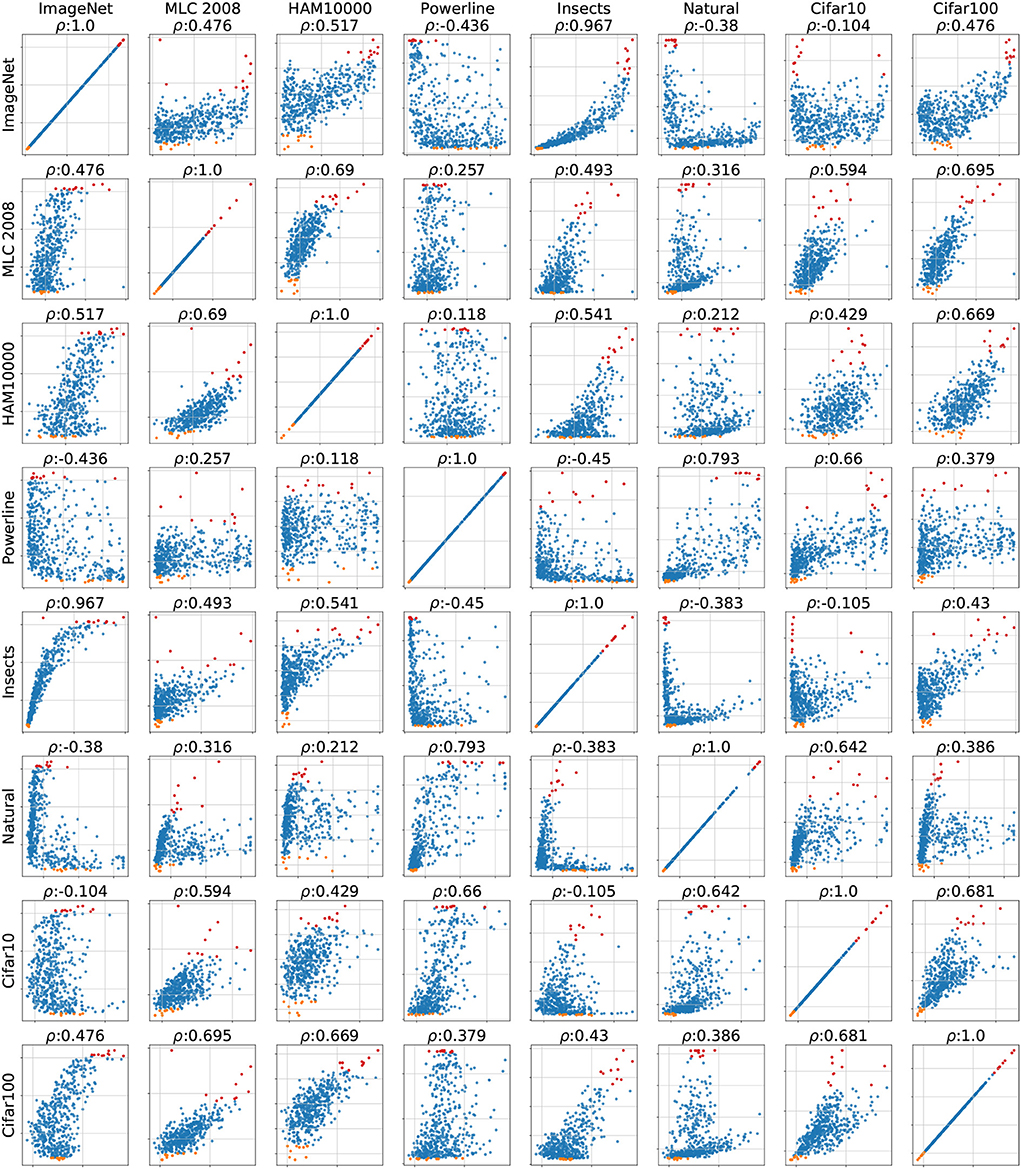
Figure A8. Matrix of error scatterplots of all datasets except Concrete (the first row replicates plots shown in Figure 3).
Block width on the other hand shows a clear pattern: almost all high-performing architectures start with a very small block width that increases across the stages. Only Powerline and Natural do not show this pattern. In block depth, we observe a similar pattern with a bit more noise. For block depth, Powerline, Natural, Cifar10 and Cifar100, no such trend of increased parameter values toward the later stages is observed. This reinforces the idea that block width and block depth greatly impact an architectures performance and their optimal choices are dataset dependent.
This post was originally published on 3rd party site mentioned in the title of this site